Hash Table With No Collisions When You Know the Keys
Hash Tables, Hashing and Standoff Handling
In continuation to my information structure series, this article will encompass hash tables in data structure, the cardinal operations of hash tables, their complexities, applications of hashing, the various types of collisions and how to handle them. You lot tin read the other topics in this series:
- Stack Information Structure
- Queue Data Structure
Earlier going into Hash tables, nosotros need to empathize the concept of hashing and hash functions.
So what is Hashing?
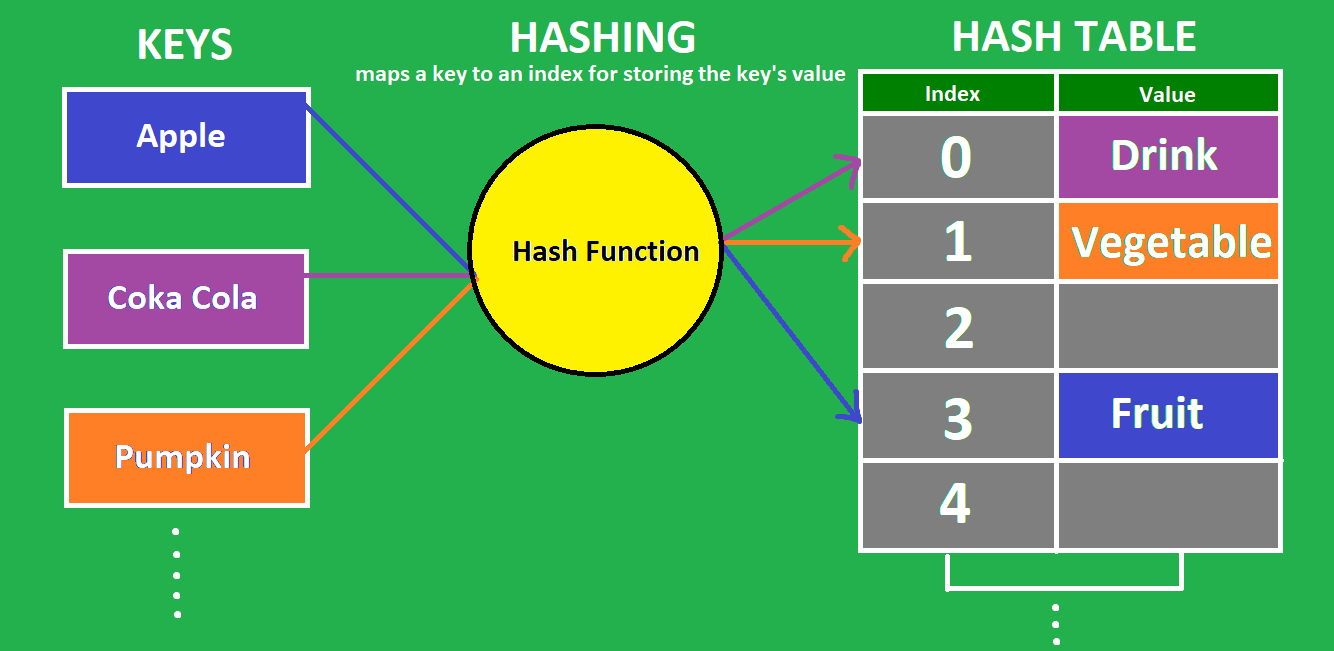
It is the procedure of converting a given cardinal into another value, with the assistance of a hash function. A hash office is nothing but a mathematical algorithm which helps generate a new value for a given input. The result of a hash function is called a hash, or a hash value.
Let's quickly learn what properties a hash function should have, to be called a adept hash function:
- Efficiently computable
- Should uniformly distribute the keys
We can always write our ain hash functions merely it is recommended non to, for there are really good hash functions already out there.

Hash Tables
A hash table is a data structure that implements an associative array abstract information type, a structure that can map keys to values. A hash table uses a hash function to compute an index, also called a hash code, into an array of buckets or slots, from which the desired value tin exist institute. — Wikipedia
In a hash table, every key is unique. We should use this data construction when the ordering and sorting of data is not needed, because the order of data is non retained here.
Hash tables must support 3 fundamental operations:
- Insert(key,value) -> Adds an item to the hash tabular array.
- get(cardinal) -> Fetches the value with the help of the given key.
- delete(central) -> Removes a value with the assist of the given fundamental.
These operations should ideally execute in O(one) time. By calculating the index of a given key very fast, hashing on boilerplate ensures a abiding time decision on where to insert into or delete/fetch from, in the hash tabular array. However, in the worst case, these operations can be of O(north) but we volition discuss that a flake later.
How does hashing assist accomplish such fast storing, removing and searching of data?
A hash table stores information in cardinal-value form. During insertion for a provided key, a hash part converts the key into an index of the hash table. The value is then stored at that alphabetize. The hash function tin produce an index that has already been used in the table, which is chosen a collision. We will talk over how to handle collisions shortly. It is due to this hash part that we are directly computing the location of a data in the table that ensures the fast operational times of this information structure.
Applications of Hashing
- Implementing hash tabular array, hash map, python's lexicon, unordered set
- cryptography: A cryptographic hash function produces output from which reaching the input is almost impossible. This property of hash function is called irreversibility. Instance of a cryptographic hash function is the pop SHA256 algorithm.
- Password verification
- Compiler operations
- Pattern searching algorithms like Robin Carp algorithm
Collisions and How to Handle Them
Two or more keys can generate same hash values sometimes. This is called a collision. A collision can be handled using various techniques.
Dissever Chaining Technique
The idea is to brand each cell of the hash table point to a linked list of records that have the aforementioned hash function values. It is uncomplicated just requires additional retentivity exterior the table. In this technique, the worst case occurs when all the values are in the same index or linked list, making the search complexity linear (northward=length of the linked list). This method should be used when we do not know how many keys will be at that place or how often the insert/delete operations will take place.
To maintain the O(one) time of insertions, nosotros make the new value as caput of the linked list of the particular alphabetize.

I am providing the code of a generic hash table implementation with carve up chaining technique, using an ArrayList of linked lists.
// this is the custom generic node course
public grade HashNode<K,V> { 1000 key;
5 value;
HashNode<K,V> next;
public HashNode(M key,5 value){
this.key = key;
this.value = value;
}
}
public form CustomHashMap<Yard,V> {
private ArrayList<HashNode<Thou,V>> bucketArray;
private int numBucket; //current capacity of list
private int size; // current size of list public CustomHashMap(){
bucketArray = new ArrayList<>();
size = 0;
numBucket = 10;
//we create empty chains
for(int i=0;i<numBucket;i++){
bucketArray.add(naught);
}
}
public int getSize(){
return size;
}
public boolean isEmpty(){
return size==0;
}
individual int getBucketIndex(K key){
int hashCode = key.hashCode(); //built in java hash func
int index = hashCode%numBucket;//modernistic to traverse circularly
return Math.abs(alphabetize); // since the key could be negative
}
public V remove(K key){
//we find the required alphabetize
int bucketIndex = getBucketIndex(key);
HashNode<1000,Five> head = bucketArray.get(bucketIndex);
HashNode<K,Five> prev = null;
while(caput!=zip){
if(head.key.equals(key)){
break;
}
prev = caput;
head = head.next;
}
if(caput==null){
return null;
}
size--;
if(prev!=nada){
prev.adjacent = caput.side by side;
}
//here nosotros are handling if key is first chemical element when prev Volition be null
else{
bucketArray.gear up(bucketIndex,head.next);
}
return head.value;
}
public Five get(K cardinal){
int bucketIndex = getBucketIndex(key);
HashNode<G,V> head = bucketArray.get(bucketIndex);
while(head!=null){
if(head.key.equals(key)){
pause;
}
head = head.next;
}
if(head==nix){
render null;
}
return head.value;
}
//add key value pair to hash tabular array
public void add(K cardinal, V value){
int bucketIndex = getBucketIndex(key);
HashNode<K,Five> head = bucketArray.get(bucketIndex);
//if fundamental already exists, we update the value
while(head!=cipher){
if(caput.key.equals(cardinal)){
head.value = value;
return;
}
head = head.side by side;
}
//insertion at head for o(1)
size++;
HashNode<K,V> newNode = new HashNode<>(central,value);
caput = bucketArray.get(bucketIndex);
newNode.adjacent = caput;
bucketArray.set up(bucketIndex, newNode);
//now to cheque for the load factor
if((1.0*size)/numBucket>=.7){
size = 0;
ArrayList<HashNode<Yard,V>> temp = bucketArray;
bucketArray = new ArrayList<>();
numBucket = ii*numBucket;
//we create the chains once more outset
for(int i=0;i<numBucket;i++){
bucketArray.add together(null);
}
//finally we re-create from one-time to new
for(HashNode<G,V> node:temp){
while(node!=naught){
//recursively
add(node.fundamental,node.value);
node = node.side by side;
}
}
}
}
}
Load Cistron = number of items in the tabular array/slots of the hash tabular array. It is the measure of how full the hash table is allowed to get before it is increased in chapters. For dynamic array implementation of hash table, nosotros need to resize when load factor threshold is reached and that is ≤0.7 ideally.
Open up Addressing technique
In this method, the values are all stored in the hash table itself. If standoff occurs, we expect for availability in the next spot generated by an algorithm. The table size at all times should exist greater than the number of keys. It is used when in that location is infinite restrictions, like in embedded processors.
Betoken to annotation in delete operations, the deleted slot needs to be marked in some style and so that during searching, we don't stop probing at empty slots.
Types of Open up Addressing:
- Linear Probing: Nosotros linearly probe/expect for next slot. If slot [hash(x)%size] is full, nosotros try [hash(10)%size+1]. If that is total as well, nosotros try [hash(x)%size+2]…until an available space is plant. Linear Probing has the all-time enshroud operation but downside includes primary and secondary clustering.
- Quadratic Probing: We wait for i²th iteration. If slot [hash(10)%size] is full, we effort [(hash(10)+i*1)%size]. If that is also total, we attempt [(hash(10)+ii*2)%size]…until an available infinite is establish. Secondary clustering might ascend here and there is no guarantee of finding a slot in this approach.
- Double Hashing: We use a 2nd hash function hash2(ten) and look for i*hash2(x) slot. If slot [hash(x)%size] is full, we try [(hash(ten)+1*hash2(x))%size]. If that is full too, we attempt [(hash(x)+2*hash2(x))%size]…until an available space is found. No primary or secondary clustering but lot more computation here.
Don't worry if the mathematical annotation confuses you. Let us walk through an case case. For a hash table of size 10, say our hash function hash(x) calculates index 3 for storing the data. And so here, [hash(x)%10]=iii. If alphabetize 3 is already full, linear probing gives united states [iii%x+1]=4 and we store the data at 4th index if not filled already. Similarly, quadratic probing gives u.s. [(3+1*i)%size]=four. Let's go a step further here, and assume the 4th index is now filled too. Quadratic probing then will calculate [(3+2*ii)%10]=7th index to exist used for storing the data. Try and find out what index double hashing would summate.
I am providing the code of a hash table implementation with linear probing technique, using two arrays. This implementation can exist tweaked to use quadratic probing or double hashing equally well, I volition get out that to your curiosity.
public course LinearProbing{
private String [] keys;
individual String [] values;
individual int size;
private int capacity; public LinearProbing(int capacity){
keys = new String[chapters];
values = new String[capacity];
this.size = 0;
this.capacity = chapters;
}
public void makeEmpty(){
size = 0;
keys = new Cord[chapters];
values = new String[chapters];
}
public int getSize(){
return size;
}
public int getCapacity(){
return capacity;
}
public boolean isFull(){
return size==capacity;
}
public boolean isEmpty(){
return size==0;
}
private int getHash(String fundamental){
return Math.abs(cardinal.hashCode()%capacity);
}
public void insert(String central,String value){
if(isFull()){
System.out.println("No room to insert");
return;
}
int temp = getHash(key);
int i = temp;
do{
if(keys[i]==zilch || keys[i].equals("DELETED")){
keys[i] = key;
values[i] = value;
size++;
return;
}
if(keys[i].equals(key)){
values[i] = value;
return;
}
i = (i+1)%capacity;
}while(i!=temp);
}
public String get(String cardinal){
int i = getHash(key);
while(keys[i]!=aught){
if(keys[i].equals(central)){
return values[i];
}
i = (i+ane)%capacity;
}
return "not found";
}
public boolean contains(String primal){
return get(key)!=zilch;
}
public void remove(String cardinal){
if(!contains(primal)){
return;
}
int i = getHash(key);
while(!keys[i].equals(key)){
i = (i+1)%capacity;
}
keys[i] = values[i] = "DELETED";
size--;
}
}
If it was a dynamic array implementation, we would take to cheque the load factor at some point of removal or insertion and take necessary steps. However, for simplicity of understanding I have used manifestly arrays here. Don't worry nearly the "DELETED" flags, because if you expect closely, they are overridden during insertions. Note that, there are other ways to implement the hash table with linear probing, feel free to explore them! Information technology will only sharpen your understanding.
Additional Hashing Knowledge
Perfect Hashing: A hash function that maps each different key to a distinct integer value or index of a table. Usually, all possible keys must be known beforehand . A hash table that uses perfect hashing has no collisions. It is besides known as optimal hashing.
Distributed Hashing: Used to store large data on many computers. Consistent hashing is used to determine which computers store which information. Read more about consequent hashing here.
Conclusion
In this article, I have tried to go the reader upward and running with the fundamental aspects of hashing and hash table information structure. Similar I echo in every article, to master any information structure nosotros demand to solve problems with it. Caput over to LeetCode, HackerRank and GeekForGeeks to find many problems on the topic and start solving them to earn that mastery. Too, please annotation that the lawmaking provided in a higher place tin always be optimized and has been written based on sure assumptions. I promise you have learned something from this write up. Thanks for reading!
Source: https://medium.com/codex/hash-tables-hashing-and-collision-handling-8e4629506572
0 Response to "Hash Table With No Collisions When You Know the Keys"
Post a Comment